Bonferroni correction

In statistics, the Bonferroni correction is a method used to counteract the problem of multiple comparisons. It was developed and introduced by Italian mathematician Carlo Emilio Bonferroni. The correction is based on the idea that if an experimenter is testing n dependent or independent hypotheses on a set of data, then one way of maintaining the familywise error rate is to test each individual hypothesis at a statistical significance level of 1/n times what it would be if only one hypothesis were tested. So, if it is desired that the significance level for the whole family of tests should be (at most) α, then the Bonferroni correction would be to test each of the individual tests at a significance level of α/n. Statistically significant simply means that a given result is unlikely to have occurred by chance assuming the null hypothesis is actually correct (i.e., no difference among groups, no effect of treatment, no relation among variables).

The Bonferroni correction is derived by observing Boole's inequality. If n tests are performed, each of them significant with probability β, (where β is unknown) then the probability that at least one of them comes out significant is (by Boole's inequality) ≤ nβ. Our intention is for this probability to equal α, the significance level for the entire series of tests. By solving for β, we get β = α/n. This result does not require that the tests be independent.

1 Criticisms
2 Alternatives to Bonferroni correction
3 See also
4 References
5 External links

Criticisms

While helpful when used correctly, concerns have been expressed about possible misuse and misunderstanding of Bonferroni correction (see, e.g., Perneger, 1998). First, Bonferroni correction controls the probability of false positives only. The correction ordinarily comes at the cost of increasing the probability of producing false negatives, aka reduced "power". Second, in certain situations where one wants to retain, not reject, the null hypothesis, then Bonferroni correction is non-conservative.

Alternatives to Bonferroni correction

Holm-Bonferroni method

A uniformly more powerful test procedure (i.e. more powerful regardless of the values of the unobservable parameters) is the Holm–Bonferroni method. However, current methods for obtaining confidence intervals for the Holm-Bonferroni method do not guarantee confidence intervals that are contained within those obtained using the Bonferroni correction. A less restrictive criterion that does not control the familywise error rate is the approximate false discovery rate which does not require ordering the p-values, then using different criteria for each test.

Šidák correction

A related correction, called the Šidák correction (or Dunn-Šidák correction) that is often used is 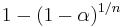$1 - (1 - \alpha)^{1/n}$

This correction is often confused with the Bonferroni correction. The Šidák correction is derived by assuming that the individual tests are independent. Let the significance threshold for each test be $\beta$ ; then the probability that at least one of the tests is significant under this threshold is (1 - the probability that none of them are significant). 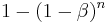Since it is assumed that they are independent, the probability that all of them are not significant is the product of the probabilities that each of them are not significant, or $1 - (1 - \beta)^n$ . Our intention is for this probability to equal $\alpha$ , the significance level for the entire series of tests. 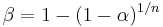By solving for $\beta$ , we obtain $\beta = 1 - (1 - \alpha)^{1/n}$ .

For example, to test two independent hypotheses on the same data at 0.05 significance level, instead of using a p value threshold of 0.05, one would use a stricter threshold equal to 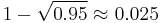$1-\sqrt{0.95}\approx 0.025$ . Notably one can derive valid confidence intervals matching the test decision using the Šidák correction by using 100(1 − α^1/n)% confidence intervals.

The Bonferroni correction is a safeguard against multiple tests of statistical significance on the same data falsely giving the appearance of significance, as 1 out of every 20 hypothesis-tests is expected to be significant at the α = 0.05 level purely due to chance. Furthermore, the probability of getting a significant result with n tests at this level of significance is 1 − 0.95ⁿ (1 − probability of not getting a significant result with n tests).

The Šidák correction gives a stronger bound than the Bonferroni correction, because, for 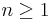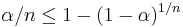$n \ge 1$ , $\alpha / n \le 1 - (1 - \alpha)^{1/n}$ . But the Šidák correction requires the additional condition of independence. Previously, because the Šidák correction requires fractional powers (i.e. roots), the computationally simpler Bonferroni correction was often preferred instead. Now, inasmuch as computing fractional powers is trivial, preference of the Bonferroni method is due in part to tradition or unfamiliarity with the Šidák method. Additionally, the results of the two methods are highly similar for conventional significance levels (between .01 and .10).

Dunnett's correction

Dunnett (1955, 1966; not to be confused with Dunn) described an alternative alpha error adjustment when k groups are compared to the same control group. This method is less conservative than the Bonferroni adjustment.

References

Abdi, H (2007). "Bonferroni and Šidák corrections for multiple comparisons". In N.J. Salkind (ed.). Encyclopedia of Measurement and Statistics. Thousand Oaks, CA: Sage. http://www.utdallas.edu/~herve/Abdi-Bonferroni2007-pretty.pdf.
Manitoba Centre for Health Policy. (2008). Concept: Multiple Comparisons, ( http://mchp-appserv.cpe.umanitoba.ca/viewConcept.php?conceptID=1049 ).
Dunn, O.J. (1961). Multiple Comparisons Among Means. Journal of the American Statistical Association, 56, 52-64.
Dunnett, C. W. (1955). A multiple comparisons procedure for comparing several treatments with a control. Journal of the American Statistical Association, 50, 1096-1121.
Dunnett, C. W. (1964). New tables for multiple comparisons with a control. Biometrics, 20 (3), 482-491 (Sep. 1964).
Perneger, Thomas V. (1998). What's wrong with Bonferroni adjustments, British Medical Journal, 316, 1236-1238 (18 April 1998, http://www.bmj.com/content/316/7139/1236.full).
School of Psychology, University of New England, New South Wales, Australia, 2000, http://www.une.edu.au/WebStat/unit_materials/c5_inferential_statistics/bonferroni.html
Weisstein, Eric W., "Bonferroni correction" from MathWorld.
Shaffer, J. P. (1995). Multiple Hypothesis Testing. Annual Review of Psych., 46, 561–584.
Strassburger, K, Bretz, Frank. (2008). Compatible simultaneous lower confidence bounds for the Holm procedure and other Bonferroni-based closed tests. Statistics in Medicine, 27 (24), 4914–4927, (http://doi.wiley.com/10.1002/sim.3338 ).